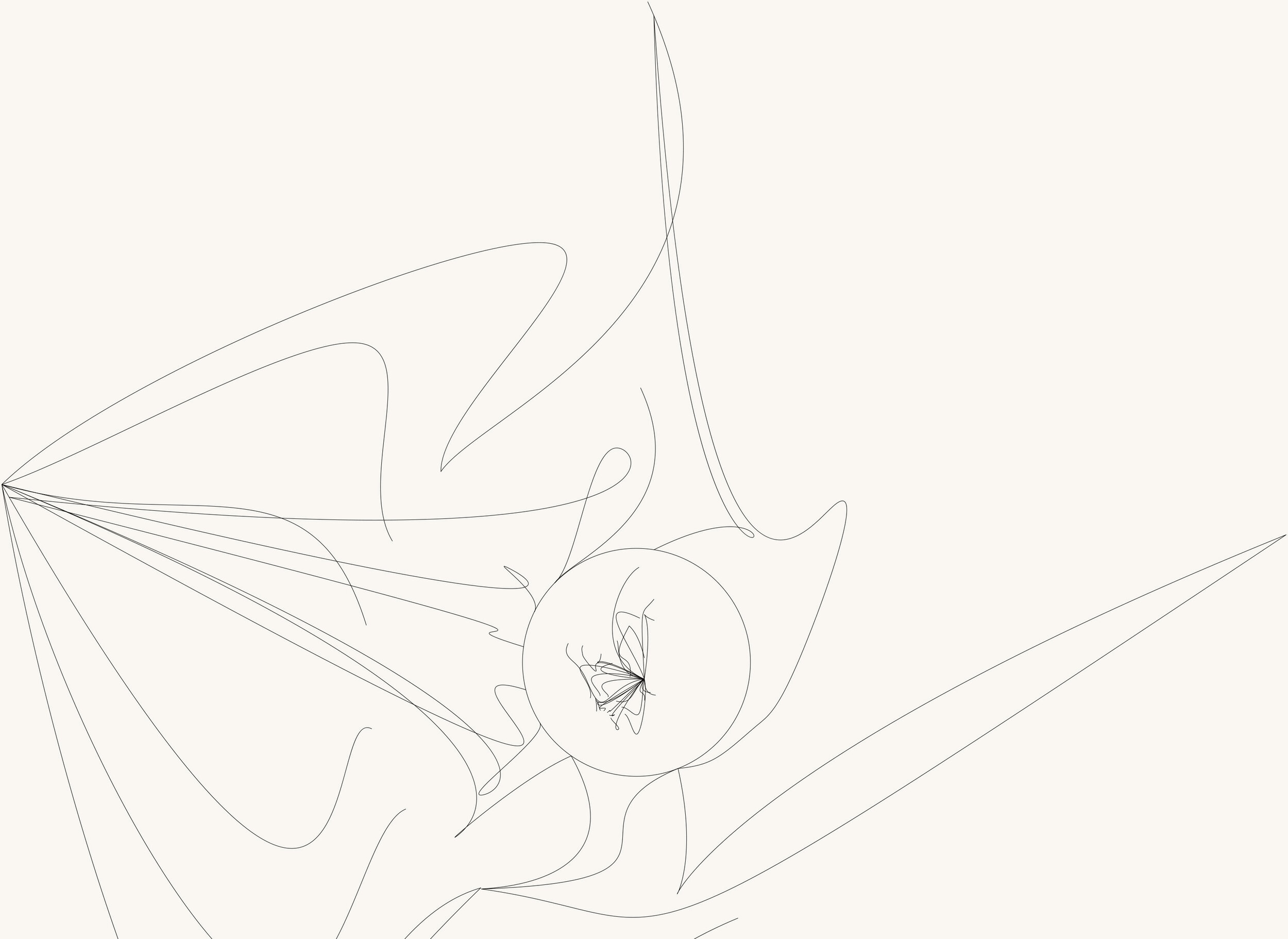
Über die Elastizität von Grenzen …
Die mathematischen Grundlagen zu diesem Projekt wurzeln in der aktuellen Forschung zu abstrakten Clusteralgebren, erlauben aber auch einen graphischen Zugang mittels Friesmustern.
Deren Interpretation als sogenannte topologische (d.h. gummiwandige) Triangulierungen inspirierte eine ästhetische Auseinandersetzung mit der Elastizität von Grenzen und Einschränkungen.
Ein dabei erschaffenes Musikstück – dem visuelle Kompositionen vorangegangen sind – spricht quasi typologisch mittels Singstimmen, Instrumenten bzw. Electronics an, ohne dass die Genesis für das Hör- und Seherlebnis notwendig wäre. …
Drei Punkte verbinden
Ausgangszeichnung
Mathematiker_in Karin Baur
The above picture shows a topological triangulation of corner points on an annulus, the area confined between an inner and outer circle.
There must be a balance between the outer and inner circles, in this case it is 13 triangles, and 13 points, they match!
You can know if you’ve missed a triangle, because the numbers of points and triangles won’t add up.
It is possible to read this diagram in a myriad of ways, in particular when an artistic, intuitive viewpoint bends the rules of topolocial triangulations themselves like rubber.
In geometry, a triangulation is a subdivision of a planar object into triangles. Topological triangulations do not require edges to be straight – like triangles in school. Rather, any non-intersecting edges connecting three corner points are considered to form triangles and thus a topological triangulation.
Another intuitive name is rubber geometry, since lines may be arbitrarily reshaped as long as they don’t intersect.
The exhibition presents various possibilities, for instance, where 5 singers surround a flute player in the middle, and attempt to communicate with each other through their voices and instruments – and to consider the diagram below, it offers thoughts surrounding the complexities of an act of intuition!
Klemens Fellner
Weiterentwicklung Komponist_in Tamara Friebel
The picture starts with a triangulation of an annulus: the blue curves subdivide the annulus into smaller regions which all have three sides, we call them triangles even if the regions look not like triangles we know from classical geometry. We then count the number of triangles meeting at the five white points on the outer boundary - this gives the numbers 7,4,3,1,4 (starting at the white vertex on the left, going around anti clockwise).
These five numbers (7,4,3,1,4) are written in a lattice of number, a so-called frieze pattern:
One starts by repeating the five numbers forever, to form a a horizontal strip, below a strip of 0’s and a strip of 1’s.
Then we form new rows using these numbers with the following rule: multiply two neighbours together, subtract 1 and then divide by the number in the middle above these two. The result is still an integer, a positive number. Such patterns were first introduced by H.S.M. Coxeter around 1970 and have become very popular in recent years as they appear in a very active research area in algebra/combinatorics.
The numbers in the frieze pattern grow very fast and this growth is governed by a parameter, the number 107 in the example. The frieze pattern is also characterised by the quiver Q which is directly associated with the triangulation of the figure.
Karin Baur




